RESOURCES
> EIS > FITTING CIRCUITS > CHI-SQUARED
 When we hear about
"least squares," it is X� that is
being minimized. What is it? And how can I relate its value to a
"goodness-of-fit" that I can understand? When we hear about
"least squares," it is X� that is
being minimized. What is it? And how can I relate its value to a
"goodness-of-fit" that I can understand?

MORE
 If we are trying to fit some data, y, to a known function, f(x),
we can write chi-squared as (See Numerical Recipes in C,
Chapter. 15)
If we are trying to fit some data, y, to a known function, f(x),
we can write chi-squared as (See Numerical Recipes in C,
Chapter. 15)
 (1) (1)
In this equation,  is the standard deviation of measurement i, which may
be different for each point measured. The problem with X� as written is that
its value depends on the number of points
used! Simply duplicating all of your data points doubles the value of X�!
Consequently, I prefer to look at X�/(n-m), where m is the number of adjustable parameters in the fit, and (n-m)
is the number of degrees of freedom. If the estimates for
is the standard deviation of measurement i, which may
be different for each point measured. The problem with X� as written is that
its value depends on the number of points
used! Simply duplicating all of your data points doubles the value of X�!
Consequently, I prefer to look at X�/(n-m), where m is the number of adjustable parameters in the fit, and (n-m)
is the number of degrees of freedom. If the estimates for  are reasonable, then X�/(n-m)
should approximate unity, regardless of the number of data points, and
different data sets are easily compared.
are reasonable, then X�/(n-m)
should approximate unity, regardless of the number of data points, and
different data sets are easily compared.
In many electrochemical experiments, the current varies widely
over the course of the experiment, and it is measured by a
potentiostat that is used in the autoranged mode. This is generally true of a Tafel
experiment in a corrosion application, or in an EIS measurement over
several decades of frequency. Many of the instrumental sources of noise (e.g.,
quantization noise at the ADC, or amplifier noise in the signal chain)
lead to errors which are (approximately) a fixed fraction,  ,
of the full scale current. Because the autoranging algorithm strives to keep the measured current (yi)
close to the full scale current, we may write: ,
of the full scale current. Because the autoranging algorithm strives to keep the measured current (yi)
close to the full scale current, we may write:  . Further,
we see that with this assumption, weighting each of the points by yi
allows us to recast equation (1) as . Further,
we see that with this assumption, weighting each of the points by yi
allows us to recast equation (1) as
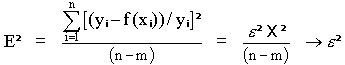  (2) (2)
Minimizing E2 is the same as minimizing X2
with this weighting assumption. However, taking the square root of E2
gives the relative error in the measured current (i.e.,  !
) That is a number most of us can understand! A value of E2 of 1e-4
translates to an average 1% error in the measured y values. [ sqrt( E2
) = sqrt( 1E-4 ) = 0.01 ==> 1% ] !
) That is a number most of us can understand! A value of E2 of 1e-4
translates to an average 1% error in the measured y values. [ sqrt( E2
) = sqrt( 1E-4 ) = 0.01 ==> 1% ]
|